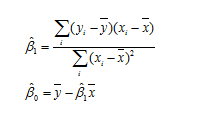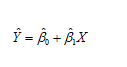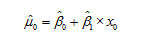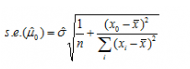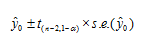Packages for SVM/Neural
Maptpx: Posterior maximization for topic models(LDA) in text analysis.
Packages for SVM/Neural:
Kernlab: Kernel-based machine learning methods for classification, regression, clustering, novelty detection, quantile regression and dimensionality reduction.'kernlab; includes Support Vector Machines, Spectral Clustering, Kernel PCA, Gaussian Processes and QP solver
Neuralnet: Training of neural networks using backpropagation, resilient backpropagation, allows flexible settings through custom-choice of error and activation function.
Packages for Twitter:
twitter:It provides an interface to the Twitter web API.
base64enc: It provides tools for handling base64 encoding. This is more flexible than the orphaned base64 package.
Httpuv: It provides protocol support for handling HTTP and WebSocket requests directly from R.It is a building block for other packages.
Manual calculation of Confidence interval and Prediction interval
Formulae used to calculate ‘beta0 hat’ ( Bo } and ‘betai hat’ { B ) values are
Here y is output column, x is input column y, is each observation in output column, ¥ is the average
of output column, x, is each observation in the input column and x is the mean of the values in the
input column
The formula to calculate predicted value of ¥ ( ¥)
Y hat = predicted value i.e. “Y hat’ = beta not hat + beta one hat times X
Substitute betaO hat and beta hat values in the above equation to get the predicted Value
Computing the estimated value and standard error
Formula for Estimated Value
Formula for Standard error
To find Estimated value u0= B0+B1 X x0 from the said equation
substitute B0 and B1 values in the given equation
and consider any one of the input observation and
substitute in the place of xo to obtain u0
To Find Standard error using the formula
Substitute xo, x1, x values in the above equation where these values are already known
Here is residual standard error
The formula for
n is number of observations and n—2 is the degree of freedom (‘2’ because we have 2 coefficients in this case namely B0 and B1 :)
Substitute residual standard error in the above formula for s.e. and obtain the estimated
standard error
Formula Confidence interval at 95%
By substituting the values in the above equation, we will get two values which will be the lower and the upper limits of Confidence interval
For ; we need to find the student's t values for 95% confidence and n-2 degrees of freedom
(‘2’ because we have 2 coefficients in this case namely B0 and B1)
Formula prediction interval at 95%
Formula to calculate prediction interval is
Similar to computing the confidence interval in the above equation we will find s.e .(¥o) and
substitute the value in the second equation thereby getting the prediction values at 95%