In real life, most of the events cannot be predicted with TOTAL certainty, and hence the possible outcomes are often expressed in terms of probability which is nothing but the answer of “How Likely these events are to happen”.
|
Probability of an event happening = |
Number of ways event can happen |
|
Total number of outcomes |
A. For the following types of events, it is easy to express the probability: -
- In tossing the coin (Mutually Exclusive), either getting Head or Tail would be 50%, as there are only two probable outcomes (Head or Tail, assuming coin will not stand vertical)
- When tossing two coins, result of first flip does not influence the outcome of second flip as these two events are Independent of each other (Independent Events)
- But now If we were to draw 2 cards from a deck, then probability of first card being queen would be 4/52 or 1/13. As there are 4 queens in deck of 52 cards.
And if we do not replace this card back in the deck then probability of second card to be queen would be 3/51 (As first queen is sitting outside), or 4/51 (May be the first card is not a queen).
This means probability changes when the events are dependent on each other i.e. the outcome of one event influences the likelihood of the other event.
- With the events points mentioned above in mind, let us look at the probability of an event (happening), given that it has some relationship to one or more other events.
If I ask you the following 2 questions
- What is the probability that one will have fever?
- What is the probability that one will have fever given the person has cold and cough?
Answers are different for both.
The second question is related to understanding conditional probability and it is an expression of how probable one event is, given that some other event occurred.
You may be wondering on why conditional probability is being emphasized upon. But if I tell you that it is used primarily in Medical sciences and Machine learning (for e.g. identifying Spam mails and pushing the same to Spam folder without any manual intervention) then I am sure that there is 100% probability of you googling about Thomas Bayes (1701-1761) who was the creator of this theorem, which was published posthumously in 1763.
|
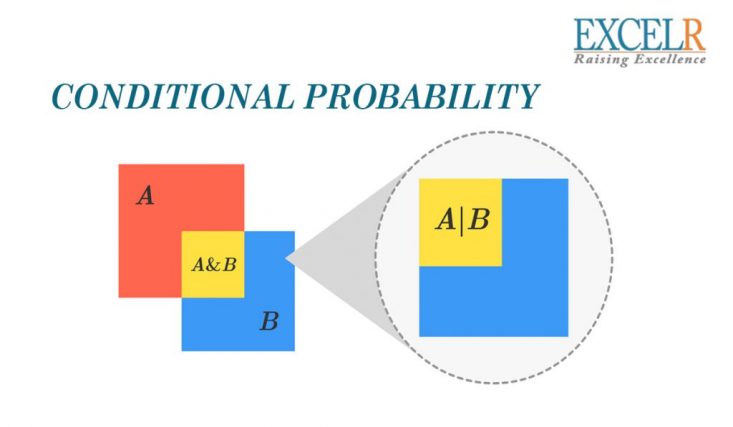
REPRESENTED AS: -
READ AS: - If the event of interest is A and the event B is known then the “conditional probability of A given B”, or “the probability of A under the condition B”, is usually written as P(A|B) defined as the quotient of the probability of the joint events A and B, and the probability of B. |
Here is a very simple example to get the feel of above formula and description
Month of September is the last month of monsoon in India, probability of Rain in that month is 30%. And cloudy mornings in September is not that uncommon, say 40% of times people in India do observe cloudy weather and if rain happens then there is 50% chance that people will observe cloudy weather.
We need to find probability of Rain given “morning is cloudy”.

Another example which will give even nicer hold on formula
There is a toy factory having 3 machines A, B and C. Toys manufactured by machine A, B and C are 60%, 30% and 10% respectively. Also, the defective toys produced by machine A, B and C are 2%, 3% and 4% respectively.
Let us solve two questions: -
- What is the probability of defective toys?
- What is the probability of selecting the defective toy from the machine C.
Solution: -
Let
A: - Toy manufactured by the machine A
B: - Toy manufactured by the machine B
C: - Toy manufactured by the machine C
D: - Toy is defective
Following statistics are given: -
|
P(A) |
Probability that the toy is made by machine A |
0.60 |
|
P(B) |
Probability that the toy is made by machine B |
0.30 |
|
P(C) |
Probability that the toy is made by machine C |
0.10 |
|
P(D|A) |
Probability of defective toy from machine A |
0.02 |
|
P(D|B) |
Probability of defective toy from machine B |
0.03 |
|
P(D|C) |
Probability of defective toy from machine C |
0.04 |
|
P(C|D) |
Probability of picking defective toy from Machine C |
?? |
Putting the Value in the formula: -
|
P(C|D) |
P(D|C) * P(C) |
||
|
P(D|C) * P(C) + P(D|A) * P(A) + P(D|B) * P(B) |
|||
|
P(C|D) |
.04*.10 |
= |
0.16 or 16% |
|
(.04*.10 + .02*0.60 + .03*0.30) =0.025 |
Answer: -
Probability of defective toy is 0.025 or 2.5%
Probability of picking defective toy from Machine C would be 16%
If overwhelmed by equation or confused, whether to multiply or add probabilities. A probability tree makes it easier to figure out when to add and when to multiply.

Example covering Medical Test to understand the greatness of Bayes’ Theorem
Woman has a cancer if tested positive for mammogram. In entire population 1% of women have cancer and 90% of women who have tested positive for mammogram have cancer. And there are 8% of women who are false positive (False positive means incorrectly predicting the positive class. Positive class in this case is having cancer). What is the probability of woman having cancer if tested positive in mammogram?
Solution: -
Need to find: - Probability of cancer if mammogram is positive.
Following Statistics are given: -

** The one in Yellow box is derived and implies 99% of woman will not have cancer as 1% of woman are having cancer
* To know more about True Positive and False Negative you may visit my earlier post https://www.excelr.com/blog/data-science/confusion-matrix
Before we get lost in equation here is the Probability Tree for Better understanding.
Let
C indicates cancer
M indicates Mammogram.
|
P(C) |
Probability of cancer in woman |
0.01 |
|
P(~C) |
Probability of not having cancer in woman (derived value as we know 1% is having cancer) |
0.99 |
|
P(M|C) |
Probability of mammogram test positive if Cancer is there |
0.9 |
|
P(M|~C) |
Probability of mammogram test positive if Cancer is NOT there (False Positive) |
0.08 |
|
P(C|M) |
Probability of Cancer if tested positive |
? |
|
P(C|M) |
P(M|C) * P(C) |
|
P(M|C) * P(C) + P(M|~C) * P(~C) |
|
P(C|M) |
0.9*0.01 - (Probable outcome) |
= |
0.1 or 10% |
|
0.9*0.01 + 0.08*0.99 (Total Positive Events) |
Ans: -
Probability of cancer in woman who has tested positive for mammogram is 10%.
One must remember that there are several forms of Bayes’ Theorem out there, and they are all equivalent (they are just written in slightly different ways). While solving and understanding the problem statement, one must be vigilant to identify what is the event (A) & which is the condition (B).
And finally, a small Trick ABABAB = P(A|B) = P(A)* P(B|A) / P(B) to not get confused.